Home Page


About This Page

This tale starts with the exploration of strange objects such as one-sided pieces of paper, bottles with no inside/outside, a two-dimensional world called Flatland, and a consideration of what a fourth spatial dimension might be like if there was one.  It then progresses to the psychedelic era, where a couple of Harvard professors experience the loss of everything that they know as "themselves', but realized that they still existed.  Known as "the process of individuation", this phenomenon was previously described by Carl Jung, with its origins going back to the Tibetan Book Of The Dead.  Their subsequent search for an explanation led them to India, where they met with quite a few surprises.  From here, I make a quick foray into mysticism and the occult, before examining some interesting conclusions obtained during a brief study of Gnosticism and Platonic philosophy.  This all landed me squarely in the realm of eastern spiritual philosophy...which turns out to be the roots of my "tree".  This story is the "trunk" that connects these roots to the various "branches" that make up the rest of my web site.

This story explains, using logic and analytical thinking, why the world around us is not the ultimate reality, how our misguided belief that it is the ultimate reality and our consequent attachment to it gives us a mistaken view of who WE really are, and ultimately ties together the entire picture of how our everyday actions and choices affect progress on the spiritual trek we all are on in our path towards the return to our true source, actions which have consequences in the here and now -- not just in some imagined "afterlife".  It is essential reading for anyone that knows me and wants to understand what seems to be my "very weird viewpoints", but it is also highly recommended for everyone else as well, as it is my conviction that it provides an important piece  of background logic for understanding the relevance, purpose, and content of this web site - not to mention one's time on this material plane.

So grab your favorite beverage, get comfortable, and let's hit the trail!!

"MAGIC THEATER. ENTRANCE NOT FOR EVERYBODY. FOR MADMEN ONLY!"

Hermann Hesse, Steppenwolf

Studying The Topological Map
 

It all started for me in tenth grade geometry class.  While the professor was up there discussing obtuse triangles and the side-angle-side theorem, my mind was focused on way cooler things, such as Mobius strips (one-sided pieces of paper), Klein bottles (the inside of which is also the outside), a possible fourth spatial dimension, and other post-2001 Space Odyssey concepts which tended to occupy a young imaginative mind in those days.

These constructs are part of a branch of mathematics known as topology, which “is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself”. (1)

For example, a piece of string tied in a loop has the same length (circumference) whether it is laid out in the shape of a square or a circle, but in each case the area within it is different.  Perhaps the most famous depiction of this is the saying that “topologists don’t know the difference between a doughnut and a coffee cup”, as illustrated by the following:

Similarly, a cow without holes in it can become a sphere:

Although it was not identified as such at the time, some argue that the beginnings of this field were sown by a puzzle put forward by Leonhard Euler, a mathematician who also gave us the formula for calculating natural exponential decay.

Seven Bridges of Königsberg

The challenge is to cross each of seven bridges connecting a mainland to various islands once and only once.  The problem with puzzles like this one is that if one can solve it, then one obviously knows it is solvable, but how does one prove that it cannot be solved if that is the case??  Simply using a trial-and-error method would be analogous to having to rely on inductive logic, as opposed to the more rigorous deductive logic, in that it would depend on something similar to looking for a five-legged cow.  One could search for a thousand years and, never finding one, reach the conclusion that there is no such thing - until someone finds one the next day.  About the time one gives up and decides this puzzle is unsolvable, someone else may come along later and prove otherwise.

Euler's analysis provides some insight into how this may be accomplished successfully in some cases.  For example, he notes that to come and go from an island there must be an even number of bridges, except that a starting or ending point may have either one or three bridges - but there can only be two of those points.  If there are more of those, then it is unsolvable.  But a method of determining the solvability of this type of puzzle in ALL cases eluded mathematicians until the recent development of supercomputers.

However, the important thing in terms of this discussion is he found that so long as the islands/bridges weren’t disconnected and re-attached elsewhere, moving them around and twisting their positions relative to each other in any way was not a factor in whether it could be solved or not - thus establishing one of the cardinal rules for topology.

Before moving on, let us examine in closer detail a couple objects that were previously mentioned.

First, about the Mobius strip.  The reader will grasp the extraordinary nature of this object more firmly by taking the time to construct it as we go.  Start by cutting a sheet of paper into strips approximately one inch wide and taping several of these together end-to-end to form one long strip.  Now bring the ends together and tape them into a loop, after first twisting one end so that the bottom side is now facing upward.  You have created a one-sided piece of paper!!  For those who always thought such a thing was impossible, we now have our first reminder that reality isn’t always what it seems!!

Don’t believe me??  Place a segment of this loop on a table and, using a marker, start drawing a line lengthwise along the strip, pulling the paper along under the marker as you proceed (being careful not to cross over the edge to the other “side”), until you reach the starting point again.  Now take a marker of a different color and attempt to repeat this process on the other side of the paper.  What’s the problem??  You don’t have a clean unmarked side any longer??  That’s because there is only one side (and one edge, by the way) to a Mobius strip.

Of course, cutting and taping this object together violates the rules of topology, so creating one as we did is not a valid topological process.  But if we should happen to stumble upon one that is already constructed laying along the trail as we hike, we should probably pick it up and take it with us.  One never knows when something this unusual may come in handy!!

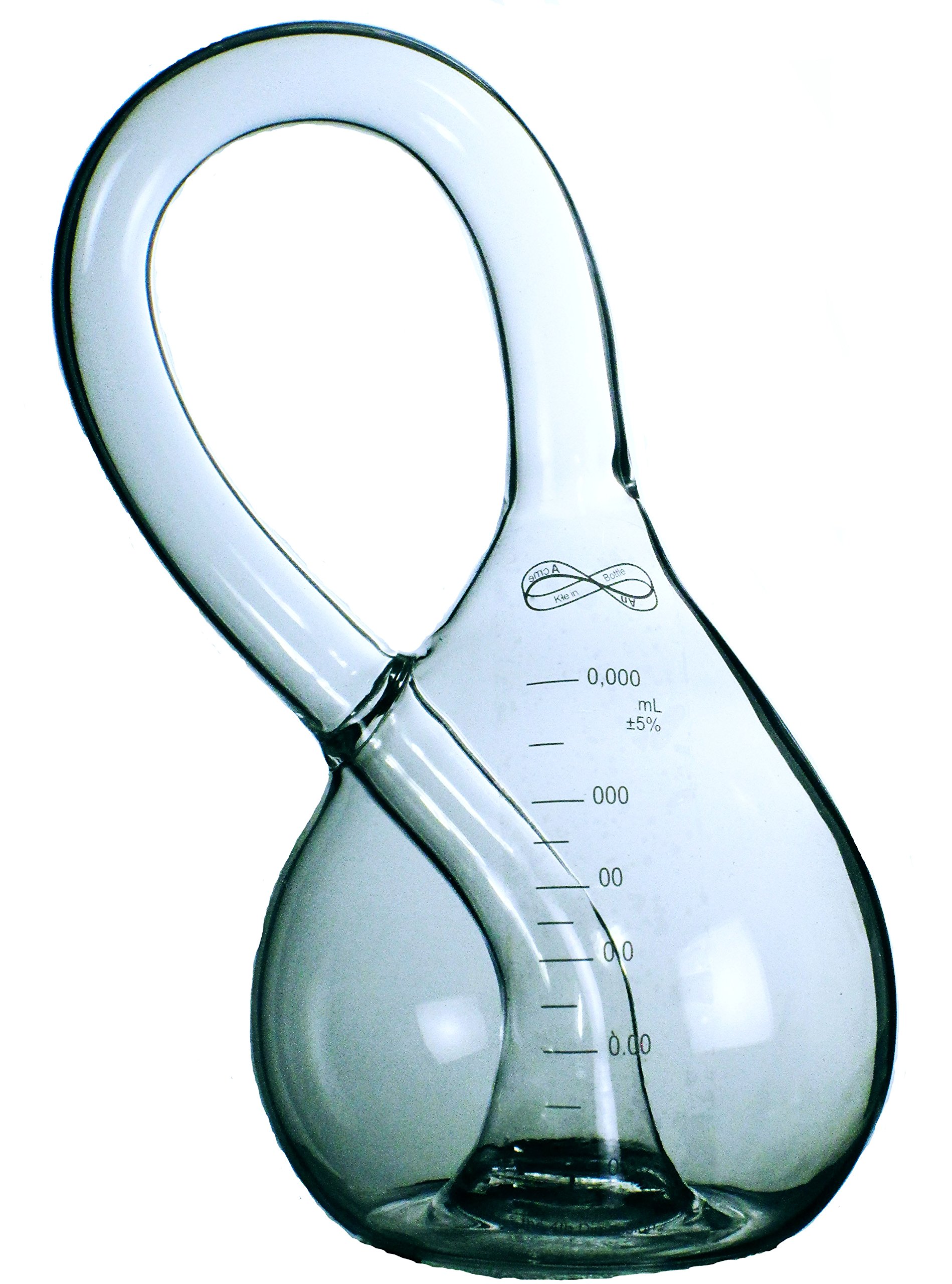The Klein bottle is a bit more complex to explain.  To do so requires understanding another principle of topology.  Imagine an ordinary glass that is cut in half from top to bottom, with a tiny man holding a flag in each hand walking along the cut edge from top left down to bottom left, then across to bottom right, and back up again.  One flag says “inside”, and always remains inside (since going around the edge at the top of the glass is a no-no).  The other flag is always on the outside.

Now, if we try the same thing with a Klein bottle, shown here, we find that as he walks along what we think would be the inside of the bottle towards the top loop, with the “inside” flag "inside" the bottle and the "outside" flag appearing to us to be "outside", then when he reaches the peak and begins traveling downward within that loop towards the bottom of the vessel, eventually rounding the base and continuing upward again, the “inside” flag is now in the space we would call the "outside", and vice versa.  We have found that the inside is the outside and the outside is inside, so this construct has no real inside or outside!!  Isn’t reality amazing??

Again, it should be noted that the smaller tube going through the surface of the more bulbous portion is also a violation of topological principles, and this is not a valid manifold of such in this dimension.  Too bad we don’t know a way of going through the bottle without cutting a hole in it!!  Please keep your eyes peeled for a method of doing so somewhere along the trail!!

Select "Next Page" to proceed to the next chapter.

-----------------

(1) Wikipedia

This page was last updated on February 7, 2023

Always remember to "Think Green" because good planets are hard to find!!  

Next Page | Top Of Page | Home Page | Email Me