Music Home | Home Page
 

Tipping The Scales
 

We have been using the term "scale" rather loosely up until now, generally referring to what is actually known as a chromatic scale -- the complete set of twelve tones contained in each octave.  However, when a pianist plays in a particular key, or practices what we call the "major" or "minor" scales, he/she only plays a subset of these tones (i.e. those represented by the eight familiar do, re, mi... notes).  This latter scale, known as the diatonic scale, is the context in which the word will be used in this section.

We must first consider how to pick and choose from the available tones in each octave those notes that we want to use in our new "lite" scale.  Today, these are dictated by applying a well-known and accepted template of whole and half-step intervals that varies slightly between the major and minor keys.  For example, there is only a half-step between the third and fourth tones, as well as between the seventh and octave tones, in a major key, where all other intervals are whole steps.  But this wasn't always the case, so it is now time to see how our current musical system actually developed over the years.

The original scale was based on simple rational numbers, and was first proposed by the ancient Greek philosopher and mathematician, Pythagoras.  Rather than creating the standard circle of fifths, as we did previously, he added a twist to the process.  Upon discovering the identity of the first three overtones of the harmonic series (2:1, 3:2, 4:3), he was convinced of the holy nature of this numerical series.  Therefore he constructed his scale using these intervals.

To see how this was accomplished, let us begin by making a standard circle of fifths.  We did this previously using frequencies, but this time let's see what happens when we use interval ratios.  We will start with a root note, of course, that we shall define as 1/1.  The octave is, of course, defined at 2/1 and the fifth is 3/2.   Now, to move up another fifth, we do not add 3/2 + 3/2 because we are dealing with exponential curves as you recall.   The laws regarding these state that mx+y = mx X my.  In other words to add two exponential values, one must multiply their component factors.  For example, 25 = 2(2+3) = 22 X 23 = 4 X 8 = 32 which equals the original 25.  So we must multiply 3/2 X 3/2 = 9/4 to find our next fifth.  But this is outside the 2/1 octave range, so we divide by 2 to get 9/8.

The next fifth is 9/8 X 3/2 = 27/16, and the next is 27/16 X 3/2 = 81/32 which we dived down to 81/64.   These are followed by 243/128 and 729/512, derived similarly.  These last two are not very simple fractions, which means they won't sound very pleasant.  Although many musicians and theorists played around with the first of these over the years, Pythagoras himself left it be.  But since the latter ≈1.434, and the holy 4/3 ratio is 1.3333..., they were close enough that he decided to alter that one.  Putting the above values in order of ascending decimal value, we have arrived at our new 8-tone diatonic scale with intervals from the tonic at:

1/1, 9/8, 81/64, 4/3, 3/2, 27/16, 243/128, 2/1

Notice that all of the numbers in the numerators and denominators of these ratios are divisible by either 2 or by 3.  You can bet the Roman Catholic church was very proud of this!!

We already know that 3/2 is called a fifth – and the reader will now see why.  The tone created at 3/2 times the root frequency becomes the fifth note of our new scale.  Likewise, the 4/3 interval can be called a "fourth", while thirds at 81/64 are a little sharp compared to a pure third at 5/4, and are known as the Syntonic Comma.  Since Pythagoreans held that the holiness of these numbers was paramount, thirds simply were not used as often as they are today.  Also note that the other tones (seconds, sixths, and sevenths) also get their names accordingly.

Later musicians, such as Aristoxenus (450 BC), argued that the judgement of the ear was vastly superior to arbitrary mathematical ratios.  One of his scales featured equal whole tones and halves of tones, leading many to believe he should be credited with inventing equal temperament.  By 2 AD, Claudius Ptolemy (the geographer) had documented a bewildering variety of scales in use, and added one of his own.  Ptolemy's position was that the ear and ratio should be in agreement (he assumed that was possible) and so adjusted some of the Pythagorean ratios slightly to generate the following interval series:

1, 9/8, 5/4, 4/3, 3/2, 5/3, 15/8, 2

This scale became the basis of a later system termed Just Intonation because it is so rich in tones with simple ratios.

These tunings held sway until well into the 14th century, despite being plagued by several problems.   For example, let's look a bit closer at the spacing between each tone in Ptolemy's intonation, as opposed to the ratio up from the tonic.  Remember that the interval between the tone at 9/8 and the root is found by dividing (not subtracting) the two, and so is calculated as 9/8 divide by 1, which is 9/8.  Similarly the next interval is 5/4 (the third tone) divided by 9/8 (the second), or 10/9.  Then 4/3 (the next tone) divided by 5/4 yields the next interval, and so forth, until the following sequence of interval spacing is determined between each successive interval:

9/8, 10/9, 16/15, 9/8, 10/9, 9/8, 16/15.

This variation in spacing means that transposing to a different key signature was impossible, because moving up one note in one particular case might mean a shift of 9/8, while in another case it might mean a shift of 10/9 instead.

At least the Pythagorean scale did not suffer from this huge flaw.  Its interval spacings were as follows:

(9/8)/1 = 9/8    (81/64)/(9/8) = 9/8    (4/3)/(81/64) = 256/243

(3/2)/(4/3) = 9/8    (27/16)/(3/2) = 9/8    (243/128)/(27/16) = 9/8

2/(243/128) = 256/243

Notice the identical spacing of most of the intervals, while the two 256/243 intervals are basically half steps:

256/243 x 256/243 ≈ 1.11 ≈ 1.125 = 9/8)

And voila!!  This sequence is the same one we still use today, where a major scale is played using the following intervals after the initial tone: whole step, whole step (this is the third), half step (fourth), whole step (fifth), whole step (sixth), whole step (seventh), half step (octave).  A minor key varies from this formula in that the third, sixth, and seventh tone is flatted by one half step.

At this point, transposing up a whole step from a half-step tone in either system lands one right smack between two whole tones.  Thus, the need to divide all the whole intervals into half steps eventually became apparent, even though most of these extra tones will not be used when playing the diatonic scale of any one particular key.  And guess what??  Adding semitones between each whole tone will lead us back to our original 12-interval octaves!!  

Imagine that!!  But there's more!!  We don't need to add these semitones (which became the black keys on the piano) between the two that are already half-steps  – thus explaining why there are two directly adjacent white keys in those places on our piano!!

These tunings (and they are called tunings instead of temperaments because they allow the comma to fall where it may) are easy to explain and to tune.  But when one digs into the details of their interval relationships, one finds that they leave a lot of notes in odd positions.  They were, however, quite satisfactory for music written in the old modes (primitive key signatures derived without the use of sharps/flats), preceding our major and minor scales.

Defeating The Comma

It is now time to address in detail how these and other more recently evolved tunings and temperaments attempted to resolve the really big problem – one that has been mentioned repeatedly, but which had not yet been fully resolved at this point in history.  You got it – the dreaded Pythagorean Comma!!

To fully understand how this was dealt with in each of the systems we want to discuss, it will be helpful to introduce a new unit of measurement – the cent.  Cents are linear units, and can thus be added normally.  One cent represents one twelve-hundredth of an equal-tempered semitone, and can be calculated as:

c = 1200 log2(f2/f1) = (1200 log (f2/f1))/log 2

The values in cents for most of the intervals discussed so far, and a few we haven't, are provided in the table below:

Notice how easily the major second, for example, can be calculated using this method.  In order to obtain this interval, one would tune up one pure fifth, and then tune a pure fourth down, because (3/2)/(4/3) = 3/2 X 3/4 = 9/8.  This may now be described as 702 - 498 = 204 cents.

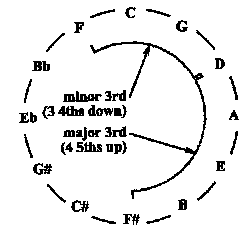Since seven octaves would be 7 x 1200 = 8400 cents, and twelve fifths is 12 x 702 = 8424 cents, we can define our Pythagorean Comma (also called the Ditonic Comma) as a difference of 24 cents. 

Similarly, the Pythagorean third may be derived by taking four pure fifths, and then subtracting two octaves (reference the figure) either calculating it as:

(3/2) X (3/2) X (3/2) X (3/2) X (1/2) X (1/2) = 81/64

or by using this simpler method:

(4 x 702 = 2808 cents) - (2 x 1200 = 2400 cents)

The third thus formed is 408 cents.   Because a pure third is only 386 cents, the Syntonic Comma is found to be 22 cents too wide – which makes it quite harsh.

What constitutes a harsh interval depends on the particular interval involved.  The limit for thirds is generally considered to be about 22 cents; fifths sound bad at about 11 cents.  But this is based on older temperaments, as well as what was considered satisfactory to them at the time, so factoring in the precision tuning inherent in our modern technology, that tolerance level may not be identical today.

Portraying these tunings with the circle of fifths helps us to readily discern the nature of their thirds and fifths, not to mention the distribution of the wolf fifth.  As a case in point, the circle of fifths for Pythagorean tuning may be depicted as shown in the following figure. 

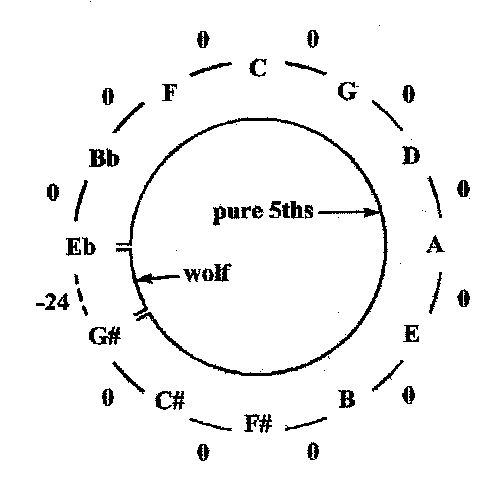Of course, they did not have sharps/flats back then, so this actually represents how it would be arranged today with semitones added.  Tuning starts at Eb and the entire comma is placed between G# and the final Eb, as outlined in Pierre Lewis' treatise, Understanding Temperaments (other authors specify alternate locations for it).

All thirds, except those that include the wolf interval, will be Pythagorean thirds (since they are equal to 408 cents, as calculated above), and will therefore sound quite tense.  However, the four major thirds that include the wolf interval will be 408 - 24 = 384 cents, which is nearly pure (only 2 cents flat)!!

Since a major third is two whole steps up from tonic, a minor third is one and a half steps up because it is a half step lower.  If C is the root, then the minor third is Eb, and looking at the circle, we see that Eb is three tones to the left of C.  Since 4/3 is a fourth, and (3/2) X (4/3) equals an octave (2/1), moving down a fourth is the same as moving up a fifth.  Therefore, moving 3 fourths counter-clockwise to reach Eb yields:

498 X 3 = 1494 → 1494 - 1200 (to bring it into the proper octave) = 294 cents

This is about 22 cents shy of a just minor third, which sits at 6/5 → 316 cents.  Notice that because moving 3 fourths counter-clockwise on the circle is the same as moving up nine fifths, most of these will contain the wolf interval. This is at (9 X 702) - (5 X 1200) - 24 = 294, while the few that don't will be sweet (at 318).

An obvious question that may arise here is in regards to why the wolf interval doesn't change with the key signature used.  One reason might be that if Eb was lowered in one case, and not in another, there would have to be two different keys on the piano for playing the "same" note.  And this would be true for all the other tones as well. 

What a mess that would be!!  So apparently, from what I can tell, the comma stayed in one location regardless of the key signature used.

In summary: except for one wolf fifth, all intervals within Pythagorean tuning are usable, if not pleasant.  In the common keys, the thirds will be harsh, which makes this tuning unsatisfactory for tonal music; but it can be quite effective for medieval pieces where the tenseness of the thirds was musically important.  Around 1400, the four nearly pure thirds were put to good use by placing the wolf between B and F# (aka Gb).  The sharp keys (the right half of the circle – today these keys all have sharps in them) now moved to the new Renaissance ideal (stable thirds), while the flat keys (on the left – G# is more commonly known as Ab, C# as Db, etc.) stayed with the old ideal.

It is ironic that equal temperament is in fact quite close to Pythagorean tuning, with its nearly pure fifths and fairly tense thirds, and is therefore quite effective for playing medieval music.

Moving on, it has already been pointed out that Ptolemy's tuning scheme, while wreaking havoc on those desiring to transpose music (due to differing interval sizes), does at least provide tones with simpler ratios.  But what else does it offer??  Not much, it seems – it still has the bane of a 22 cent wolf fifth (with the other 2 cents appearing elsewhere) which now must vary with the key signature.  This is because that interval is fixed by the sixth and second tones of the diatonic scale as being (5/3)/(9/8) = 40/27 instead of 3/2.  And, of course, which notes occupy the position of those tones depends on the key signature.  What a nightmare for the keyboardist!!

But what if we tried placing three different 22-cent wolf fifths evenly around the circle as shown in figure 4??  They must be compensated for, so we also add a +42 cent double-wolf fifth somewhere.  That way the total will still be equal to -24 cents. Now all thirds, except those with the diminished sixth wolf, will be pure at 4 x 702 - 2400 - 22 = 386 cents...because each will by default include one of the -22 cent wolf fifths.  The others will be totally unusable at 428 cents each.

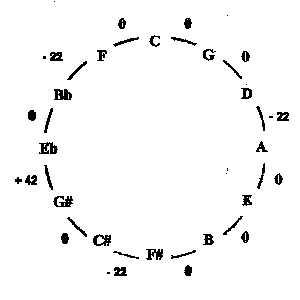While the above scheme improves most of the thirds, a huge price is paid in terms of the number of fifths that are no longer usable.  However, this was the theory behind Just Intonation.  And apparently that is all it was – a theoretical solution.  At least according to one author (Peter Lewis), who writes:

"This tuning is mostly of theoretical interest since any attempt to impose it upon fixed-intonation instruments necessarily leads to serious flaws which make it impractical. As Barbour said in Tuning and Temperament, "it is significant that the great music theorists...presented just intonation as the theoretical basis of the scale, but temperament as a necessity".

Around the 15th century, various Meantone temperaments became popular.  These systems are categorized as "regular" temperaments because all the fifths, except the wolf, are tempered by the same amount.   The idea was to maintain the purity of the thirds while improving on the fifths (compared to Just Intonation).  Peter Lewis does a good job of describing some of the main variations of Meantone, so I won't go into that here.

By Bach's time, the familiar Well-Temperament had become popular.  There were again many variations, but the basic concept was that the tones were tempered enough such that all keys were now usable, with each providing its own unique color based on the tuning of its intervals.  This was because each contained varying degrees of the wolf.   Many musicians today still favor this system due to the tonal variations it offers.  Thus it was out of a desire to prove that all keys could now be used that Bach wrote his famous Well-Tempered Clavier compositions, consisting of 24 preludes and 24 fugues – one in each of the major and minor keys.

Finally, in 1911, the first sufficiently accurate method of measuring pitch was invented, and the mathematically precise spacings of equal temperament followed shortly after.

If one looks at a chart of the frequencies in use today (as we derived in the first section), it will become obvious that the equal-tempered intervals (ignoring the semitones that were added later) correspond quite well with Ptolemy's original just ratios.  The chart below outlines the various approximate interval ratios:

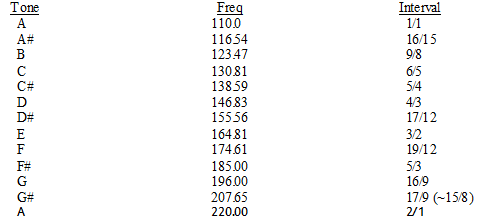
Clearly, the choice of tones used in the diatonic scale (e.g. A Major: A, B, C#, D, E, F#, G#, A and A minor: A, B, C, D, E, F, G, A) provides a great mix of the most pleasant sounding ratios, with only a couple of exceptions.   The G# (seventh) near the end, by the way, leaves one with a feeling of suspense – emphasizing that the scale is unfinished until the octave tone is played.

Besides the full major and minor scales (of which there are actually three variations), there are also subsets commonly used by musicians today.  Some scales contain jumps of three semitones or more and may contain very few notes.  An extremely common example (upon which a disturbing number of pop hits and electric guitar solos are based) is the so-called pentatonic scale, containing only five notes and two jumps of three semitones (i.e. the fourth and seventh is omitted).  In the key of C, the pentatonic scale is C-D-E-G-A.

If you arpeggiate this scale a few times (plus the C at the end: C-D-E-G-A-C, C-D-E-G-A-C), you'll probably want to start singing "I've got teardrops...".  Motown sure made a lot of money from these five notes!!  The pentatonic scale fits into almost any song because this set of notes is rarely dissonant even through common chord changes within the piece.  I learned about this technique under the guise of "the blues progression " years ago.

If you really must have an equidistant six-tone scale, there is a system called (rather appropriately) the Whole Tone Scale, which was used extensively by the jazz great, Thelonius Monk, and has continued to be popular in jazz circles.  The Whole Tone scale in C would consist of the following notes: C-D-E-F#-G#-A#.  It has a characteristically circular and bottomless feel about it, and tends to suggest offbeat scales and modes.

So there you have it...hopefully I have guided you through the maze without casualty, have answered many of your most pressing questions, and offered knowledge regarding the history of temperament beyond what was expected at the outset.  I know that my own trip into this mysterious realm led me into territory way beyond what I ever anticipated when I first began.

Now if you'll excuse me, I need to go practice...

 

This page was last updated February 12, 2023

Always remember to "Think Green" because good planets are hard to find!!  

Previous Page | Top Of Page | Music Home | Home Page | Email Me